병합 정렬

병합정렬이란?

병합(합병)정렬이란?

• '존 폰 노이만'이라는 사람이 제안한 방법
  • 일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘의 하나이다.
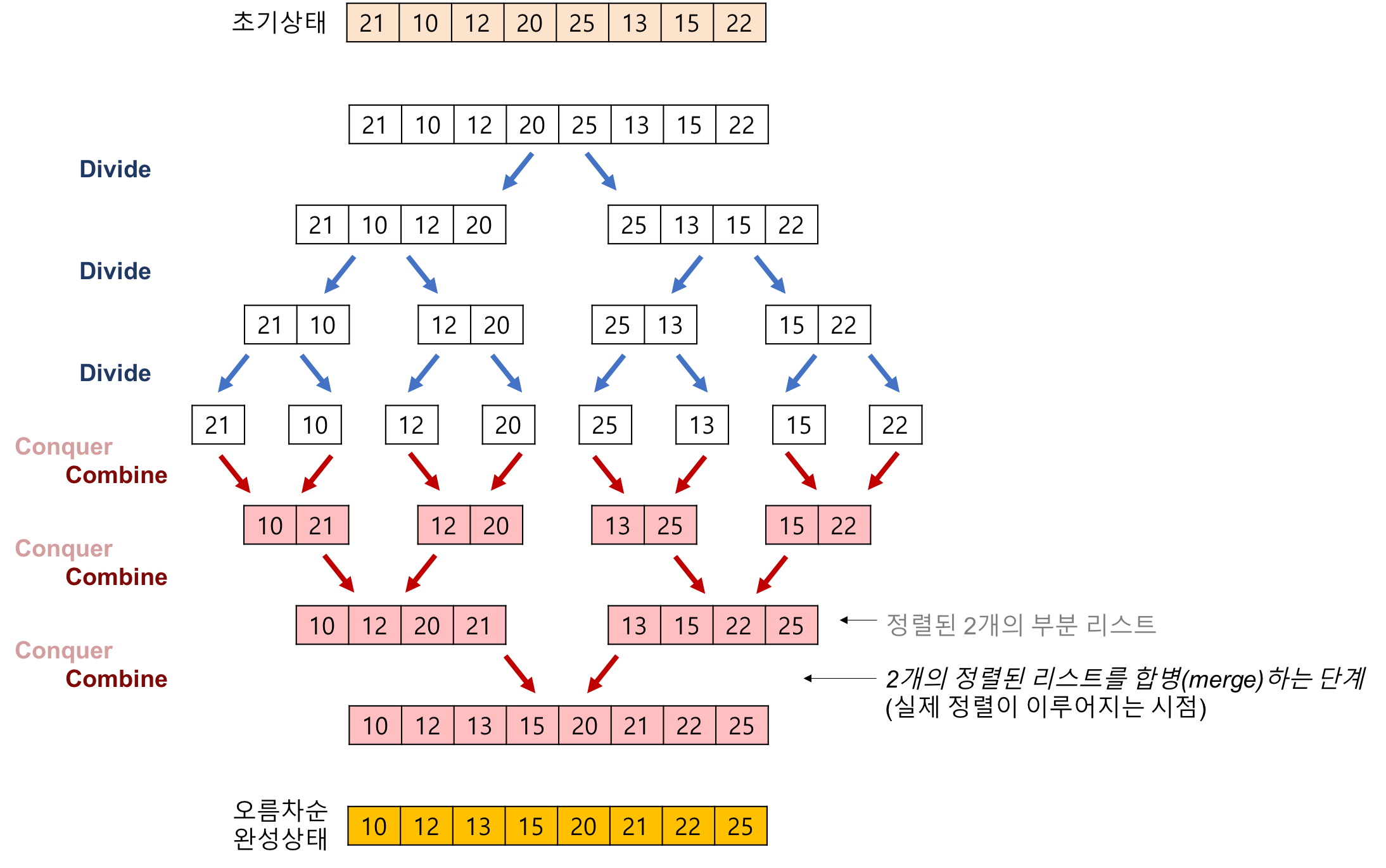
    • 분할정복(divide and conquer)방법
      • 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
      • 분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
  • 과정
    1. 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다.
    2. 그렇지 않은 경우 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
    3. 각 부분 리스트를 재귀적으로 병합정렬을 이용해 정렬한다.
    4. 두 부분 리스트를 다시 하나의 정렬된 리스트로 병합한다.

병합정렬 코드

def merge(left, right):
    result = []
    while len(left) > 0 or len(right) > 0:
        if len(left) > 0 and len(right) > 0:
            if left[0] <= right[0]:
                result.append(left[0])
                left = left[1:]
            else:
                result.append(right[0])
                right = right[1:]
        elif len(left) > 0:
            result.append(left[0])
            left = left[1:]
        elif len(right) > 0:
            result.append(right[0])
            right = right[1:]
    return result

병합정렬의 장단점

• 장점
  • 안정적인 정렬 방법
    • 데이터의 분포에 영향을 덜 받는다. 즉, 입력데이터가 무엇이든 간에 정렬되는 시간은 O(nlog2n)으로 동일하다.
    • 만약 레코드를 연결리스트로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다. -> 제자리 정렬로 구현할 수 있다.
    • 따라서 크기가 큰 레코드를 정렬할 경우에 연결리스트를 사용한다면, 합병 정렬은 퀵정렬을 포함한 다른 어떤 정렬 방법보다 효율적이다.
• 단점
  • 만약 레코드를 배열로 구성하면, 임시 배열이 필요하다.
    • 제자리 정렬이 아니다.
  • 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.

시간복잡도

• 분할 단계 - 비교 연산과 이동 연산이 수행되지 않는다.
• 합병 단계
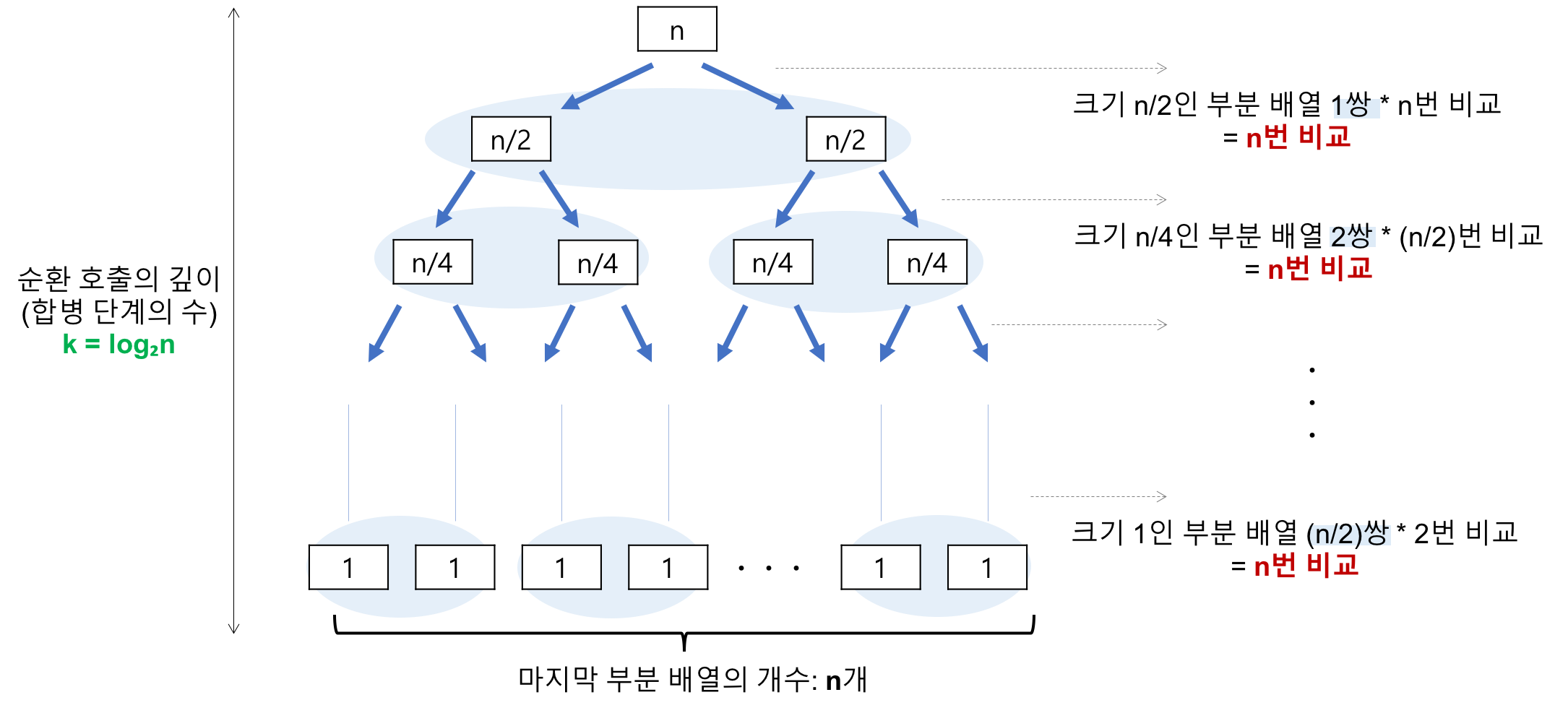
  • 병합 단계의 깊이
    • 데이터의 개수 n 이 2의 거듭제곱이라고 가정할 때 n=8의 경우 8->4->2->1 순으로 줄어들어 단계가 3임을 알 수 있다. 이것을 일반화 하면 n=$2^{k}$의 경우, k=$\log_{2}{n}$임을 알 수 있다.
  • 각 병합 단계의 비교 연산
    • 크기 1인 부분 배열 2개를 합병하는데 최대 2번의 비교 연산이 필요하고, 부분 배열의 쌍이 4개 이므로 2*4=8번의 비교 연산이 필요하다.
    • 이것이 크기가 1->2->4->8로 진행 되면서 각각 위의 경우 8번의 비교 연산이 필요하므로 이것을 일반화하면 하나의 합병 단계에서는 최대 n 번의 비교 연산을 수행함을 알 수 있다.
  • 따라서 병합 단계의 깊이* 각 합병 단계의 비교 연산=$\nlog_{2}{n}$이다.
  • 이를 빅오 표기법으로 표기하면 O($\nlog_{2}{n}$)이다.

참고 자료

• 병합정렬
• 합병정렬

면접 예상 질문

• 병합 정렬의 시간복잡도를 나타내보세요

기여자

_{Youngwoo Kim}
📦